Quantum and Post-Quantum Cryptography

In a world where political activists and dissidents get persecuted by authoritarian governments, strong cryptography is more necessary than ever. But the general public benefits from it as well. Identity theft, banking fraud and cyber bullying can happen to anybody. The most effective protection is to not make sensitive material available to anybody. Unfortunately some people have an “I have nothing to hide” mentality. But would you post your opened mail to your garden fence? Just because most people are not doing illegal activities, some information is better kept private to stay safe from the aforementioned crimes.

In times where government agencies but also black hat hackers have access to a wide variety of personal information, the best protections are transparent and mathematically proven encryption algorithms. Currently we have two main forms of encryption:

Symmetric Cryptography

Two parties (in cryptography usually called Alice and Bob) want to secretly share information between them. Alice encrypts the data with a secret key and Bob can decrypt the data with the same key. The data that is sent between them is called ciphertext. A good encryption algorithm can produce ciphertext that looks pretty much random. Changing a single bit in the data should completely change the ciphertext as well. This makes sure that an attacker that eavesdrops on the communication channel cannot determine the secret key, even if they might know parts of the unencrypted message. So far so good, or is it? The main problem is how to share the key between the communicating parties. They might sit on the opposite sides of the world. To overcome this issue, we have to make use of another form of encryption.

Asymmetric Cryptography

It uses not only one, but a public and a private key. The names already imply the secrecy of these keys. To encrypt a message, Alice uses Bob’s public key which is known to everybody. Once the message is encrypted, it can only be decrypted with the private key, which is only known to Bob. This is enforced through trapdoor functions. These are mathematical functions that can be computed easily in one direction, but not in the reverse direction. However, with enough computational power, it is still possible! Since asymmetric encryption is generally slower than symmetric encryption, it is only used to share a secret key, which is then used for symmetric encryption algorithms.

This has worked really well for the past decades. But although many researchers are working on keeping encryption safe and accessible for everybody, just as many work on breaking currently used algorithms. That is why ideally we want a way of encrypting data, which is not only safe from our current most powerful computers, but from any possible computer in the future. Here Quantum Cryptography comes into play. Correctly implemented it is unbreakable because it is protected by the laws of physics.

Quantum Cryptography

Before we learn more about this highly anticipated encryption wonderland, we have to dive a little bit into the world of quantum physics. Now a famous quote, widely attributed to Richard Feynman, says, “If you think you understand quantum mechanics, you don’t understand quantum mechanics.” Luckily we only really need to understand one simple law of quantum mechanics. Heisenberg’s uncertainty principle states that “the more precisely the position is determined, the less precisely the momentum is known, and conversely”. This is in regards to quantum particles, where any form of measuring them will inevitably result in a change of their quantum state. Going a bit further, we arrive at the No-Cloning Theorem. Because our measurement of quantum particles will alter them, we cannot make an identical copy of their quantum state. We simply don’t know what the particle was like, before we interacted with it. This is the fundamental principle behind quantum cryptography.

Quantum Key Distribution

Quantum cryptography has many different applications. The most important one and sometimes even used synonymously to quantum cryptography, is called Quantum Key Distribution. It still uses regular symmetric encryption but the secret key is shared with quantum mechanics.

BB84 Protocol

Named after the inventors Charles Bennett and Gilles Brassard, it makes use of the polarization of light. Light consists of photons which can be sent out individually from an emitter. They can also be given a polarization, which is the direction in which they oscillate. When they travel through a polarized filter, they interact with it depending on their orientation.

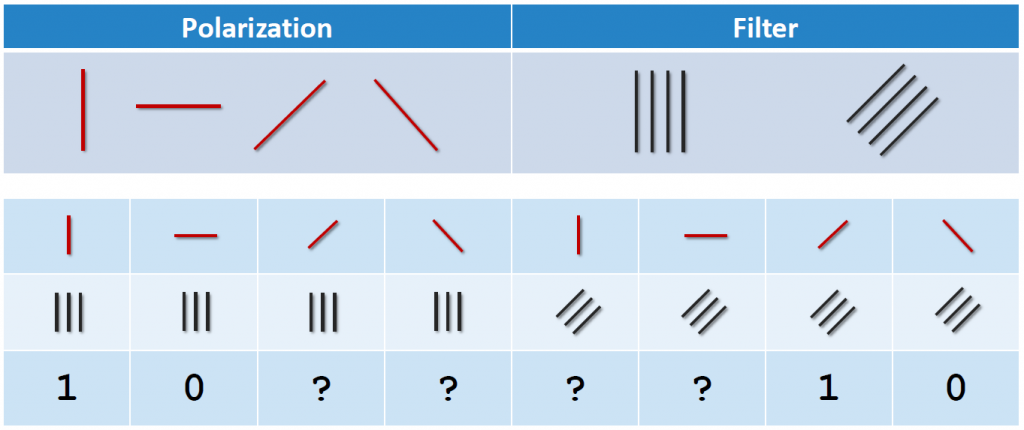BB84 Protocol photon and filter polarizations Figure 1. Interaction between polarized photons and filters

Figure 1 shows four ways of polarized photons and two different filter orientations. Photons which are aligned with the filter can pass through and be seen as light by a detector. This is registered as a 1. When the orientations are perpendicular to each other, no light will pass through. The result is a 0. But if the orientations are at a 45° angle to each other, the output cannot be previously determined. The photon will randomly pass through with a 50% chance. This property of photons can be used to generate a secret key between two parties.

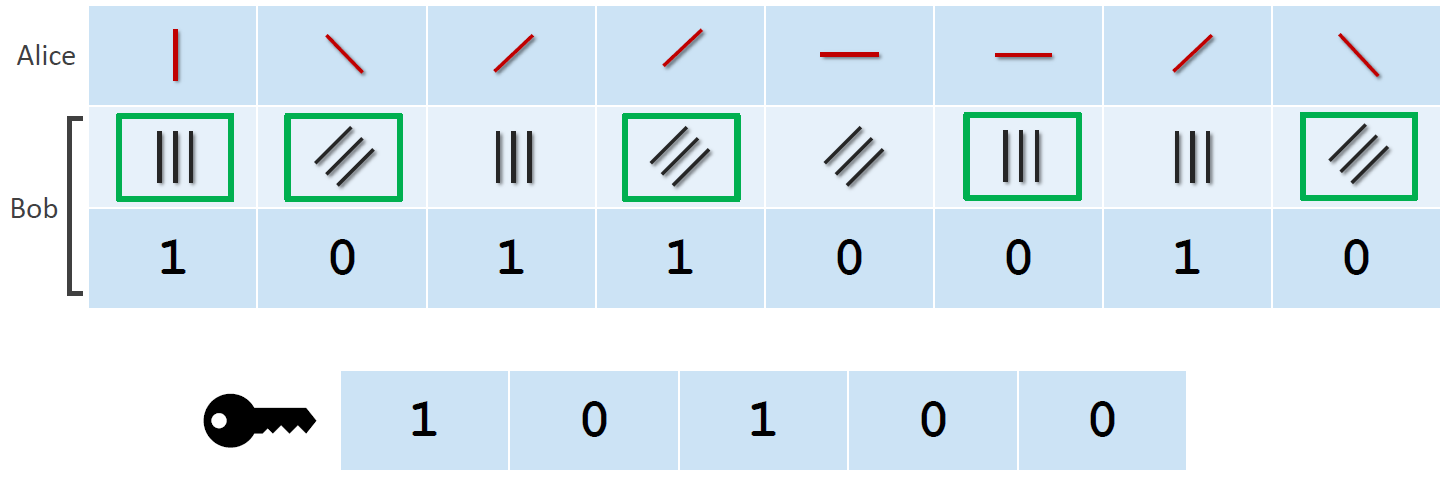
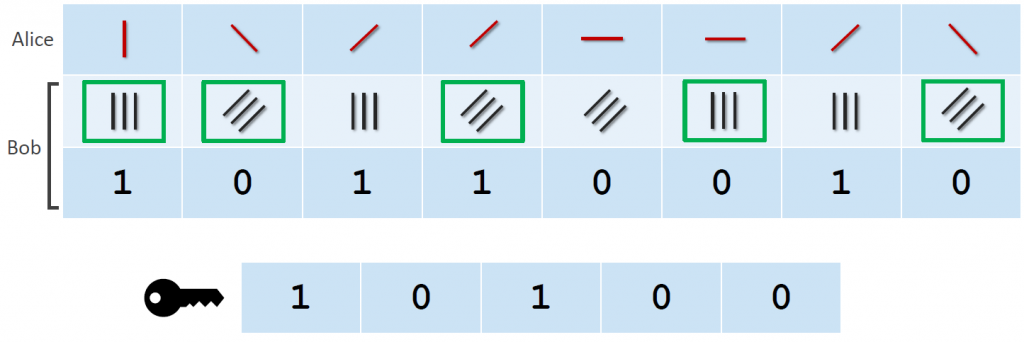BB84 Protocol key generation Figure 2. Key generation with the BB84 protocol

Alice sends photons to Bob which are polarized in a random direction (out of the possible variants). Bob chooses a random filter orientation and measures the outcome. He tells Alice which filters he used and she answers with the positions where he used the correct ones (marked in green). These have an orientation to the photon where the output is deterministic. All other photons produce a random output and are therefore worthless. The key consists of the bits that were measured by the correct filter. Alice can also calculate the key since she knows which photons she sent and what filters Bob used. An attacker cannot calculate the key because he doesn’t know the polarization of the original photons sent by Alice.

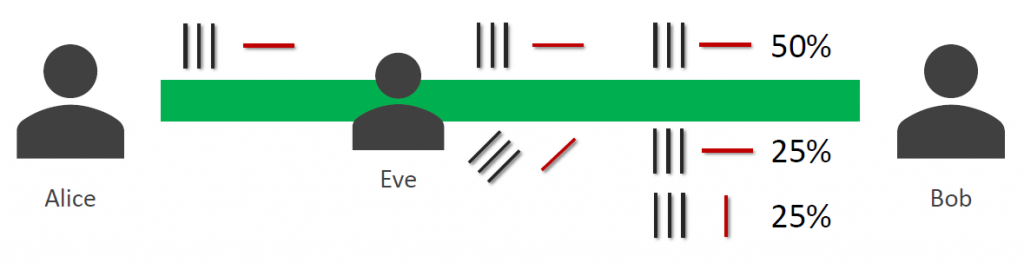BB84 Protocol Eavesdropping on quantum channel Figure 3. Eavesdropping on the quantum channel

Figure 3 shows an eavesdropper (Eve) on the quantum channel. Eve will use a random filter and send a photon to Bob, which is polarized according to the output she measured and the filter she used. Now Bob has a 75% chance to receive the outcome that was originally intended by Alice. But in 25% of the cases, the measured bit will differ between Alice and Bob. To find an eavesdropper on the channel, they have to compare parts of the key, which can then obviously not be used anymore. The quantum channel also has to be authenticated. Otherwise a Man-In-The-Middle attack is possible.

Ekert Protocol

The Ekert protocol uses quantum entanglement to distribute a key. Two quantum particles can be created in such a way that they have an entangled property, like their spin. If one particle is measured to be spin up, we know that the other one is spin down. By measuring probabilities, it can be proven that the state of an entangled property will only collapse into a fixed value once one particle is measured. Then the other particle will immediately show the opposite value, even if the particles are light years apart. This does not violate Einstein’s postulate that information cannot be transmitted faster than the speed of light, since it is not possible to transmit data via quantum entanglement. But it can be used to share a random key between two parties. This is the principle of the Ekert protocol.

Applications

Quantum key exchange has been achieved through optical fibre over a distance of 400 km and through the air over 144 km. It was also tested with a satellite connection, where the satellite sent out entangled photons. More practical applications include a bank transfer in Vienna in 2004 and the transmission of election results in Switzerland in 2007. But the main problem with using this technology over long distances is the fact that the signal cannot be repeated or routed. A direct connection between the communicating partners is necessary. This makes it difficult to use on a global scale.

Post-Quantum Cryptography

Properly implemented, our current ways of using cryptography on the internet are sufficient for today’s technology. But in the future, asymmetric cryptography is threatened by quantum computers. This form of cryptography mainly relies on three mathematical problems that are currently unsolvable in polynomial time: Integer factorization, the discrete logarithm and the elliptic-curve discrete logarithm. But Peter Shor already proposed a quantum algorithm in 1994 that can factorize integers in polynomial time. Once powerful enough quantum computers exist, current asymmetric cryptography algorithms like RSA or the Diffie-Hellman key exchange can be broken. This is a major threat to the current way the internet works. Therefore, a lot of research has already been invested into quantum safe encryption algorithms or Post-Quantum Cryptography.

Hash-Based Signature Systems

Digital signatures rely on asymmetric cryptography and are therefore also not future-proof. Hash functions however are safe from quantum computers, based on the current understanding. Using hashing for digital signatures was already invented by Ralph Merkle in 1979, but there are major disadvantages to currently used signature schemes, which is why it never became popular.

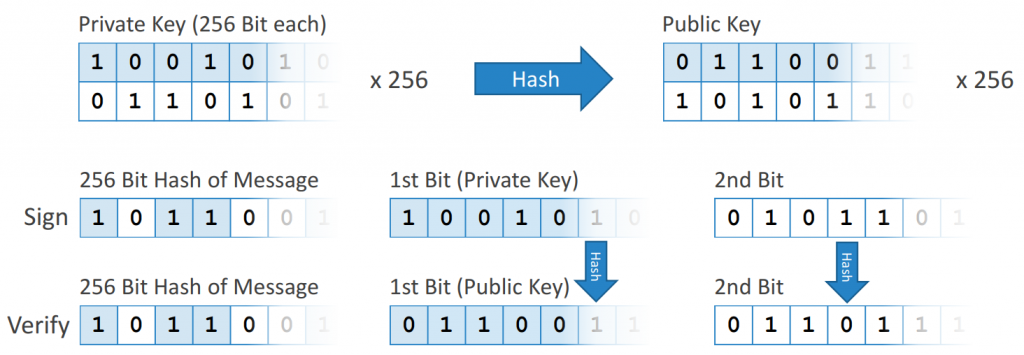Figure 4. Hash-Based Signatures

To use this signature scheme securely, the private key can only be used once, since parts of the key are revealed to the receivers. The public key is a hashed version of the private key. To sign a message, parts of the private key are sent with the message data. The receiver of the message also hashes the private key and compares it to the public key and the original message data.

Code-Based Encryption Systems

Robert McEliece invented a code-based encryption system in 1978. It uses error correcting codes. Encryption data with the public key adds errors to the ciphertext, which can be reverted with the private key. The main disadvantages are the very large key sizes of 512 kilobit in the standard configuration. There are endeavours to reduce the key size, to make this the main public-key encryption system for post-quantum cryptography.

Conclusion

Quantum cryptography makes use of the No-Cloning theorem, which postulates that quantum states cannot be identically copied. This makes it physically safe from eavesdroppers. Quantum Key Exchange allows the distribution of keys for classic symmetric encryption algorithms like the One-Time Pad. Unfortunately, a direct connection between the communicating partners is always necessary. This makes it difficult to implement on a global scale.

But quantum cryptography is not necessary to achieve encryption, which is safe from quantum computers. Although classic asymmetric encryption algorithms can be broken by quantum computers, new algorithms for encryption and digital signatures are already worked upon.

Research Questions

Quantum and post-quantum cryptography still require a lot of research to overcome their problems. Quantum computers are just now starting to become a thing, and many things are still unclear about them. These questions came to mind when researching this topic:

How can a global quantum cryptography network be implemented?
Can photons be propelled without interacting with them?
Which algorithms can quantum computers implement better than conventional computers?
Can hashing be broken by quantum computers?