It is widely known that tech companies, like Apple or Google and their partners collect and analyse an increasing amount of information. This includes information about the person itself, their interaction and their communication. It happens because of seemingly good motives such as:
- Recommendation services: e.g. word suggestions on smartphone keyboard
- Customizing a product or service for the user
- Creation and Targeting in personalised advertising
- Further development of their product or service
- Simply monetary, selling customer data (the customer sometimes doesn’t know)
In the process of data collection like this clients’ or users’ privacy is often at risk. In this case privacy includes confidentiality and secrecy. Confidentiality means that no other party or person than the recipient of sent message can read the message. In the special case of data collection: no third party or even no one else but the individual, not even the analysing company should be able to read its information to achieve proper confidentiality. Secrecy here means that individual information should be kept secret only to the user.
Databases may not be simply accessible for other users or potential attackers, but for the company collecting the data it probably is. Despite anonymization/pseudonymization, information can often be associated to one product, installation, session and/or user. This way conclusions to some degree definite information about one very individual can be drawn, although actually anonymized or not even available. Thus, individual users are identifiable and traceable and their privacy is violated.
The approach of Differential Privacy aims specifically at solving this issue, protecting privacy and making information non-attributable to individuals. It tries to reach an individual deniability of sent/given data as a right for the user. The following article will give an overview of the approach of differential privacy and its effects on data collection.
Privacy
The first questions to answer are: What is the definition of privacy? Can it be reached, if yes how? The swedish mathematician and computer scientist Tore Dalenius defines privacy as follows in 1977:
“Nothing about an individual should be learnable from the database that cannot be learned without access to the database.”
Dwork C. (2006) Differential Privacy. In: Bugliesi M., Preneel B., Sassone V., Wegener I. (eds) Automata, Languages and Programming. ICALP 2006. Lecture Notes in Computer Science, vol 4052. Springer, Berlin, Heidelberg
In other words: A collection of data or the process of collecting it violates an individual’s privacy, if an information about this very individual can be defined more precisely having insights into the collection than without it. This does makes sense at first sight: reading a collection of information should not enable you to learn about an individual’s information, otherwise its privacy would be violated.
However, the definition is too strict in context of today’s massive data collections with an increasing number of data collections holding increasing amount of information. Regarding Tore Dalenius’ definition, privacy could easily be violated associating a data source with auxiliary sources. An example for this is the Netflix Prize Challenge, in which Netflix challenged everyone interested to beat the (sum of) algorithm(s) used by them to recommend movies to a user he might like. Contestants were given an anonymized database containing reviews and ratings from real Netflix users. By executing a so-called linkage attack, a group of contestants was able to associate this anonymized data with secondary (non-anonymized) source (namely reviews from ImDb). That way they accomplished to identify individual users. With the information from Netflix they could learn more about these users than they could have without it. This violates the aforementioned definition of privacy.
Possible Approaches (?)
“Classic” approaches like encryption or anonymization seem useful at first. However, they do not solve the issue at hand that information about individuals can be deduced and associated with them.
Encrypting data and communication prevents unauthorized access. This strengthens confidentiality of data, as only authorized individuals or companies are granted access to data. Yet, an authorized party, such as the company collecting the information can attribute it to individuals easily. Furthermore, operations to gain statistical insights on collected data should either be performed on clean data. This would require decryption before every computation. Or so-called homomorphic encryption algorithms must be used, profiting from their characteristic that the decrypted result of an operation on encrypted data is equal to that one of an operation on decrypted data.
Data could be anonymized to hinder attribution of data to individuals, as the individuals aren’t identifiable in the best case. However, the party realizing anonymization needs to be trusted in performing it correctly. Also, as mentioned before de-anonymization is possible due to linkage attacks. It has happened on relatively benign information, yet also on sensitive data such as medical files. De-anonymization could be impeded reducing the resolution of information for example by storing only a month instead of a specific day or a country instead of a city. But, thereby the value or utility of the examined data is diminished.
Both encryption and anonymization won’t really prevent the problem of attribution. The approach of differential privacy however is specifically targeted at this issue.
Introduction to differential privacy
Differential Privacy is a theoretical concept and approach to preserving privacy. It gives mathematical formal definition for privacy, but does not define one specific implementation or framework. It is important to note that it does not rely on encryption at all. The overall goal is to reduce the risk that information will be used in a way that harms human rights. Moreover, it defines and tackles the tradeoff between privacy and utility of the examined information. It shall help to both…
“[…] reveal useful information about the underlying population, as represented by the database, while preserving the privacy of individuals.”
Dwork C. (2006) Differential Privacy. In: Bugliesi M., Preneel B., Sassone V., Wegener I. (eds) Automata, Languages and Programming. ICALP 2006. Lecture Notes in Computer Science, vol 4052. Springer, Berlin, Heidelberg
The concept of differential privacy deals with this trade-off, tries to formalise and even quantify it.
Method of differential privacy
The following example explains the method of differential privacy:
Suppose Alice has access to some kind of private information (for example from her customers). She is called the curator of data, as she holds it, has access to it and can control what and how it is revealed to any other party. Bob is representing anyone, who would like to gain insight to (statistic) information about Alice’s data. This could be an employee of a company collecting the information, a customer, client or partner of this company.
As Bob would like to know more about the information Alice holds, he makes a request to Alice. Alice aims at protecting her customers’ privacy. Therefore, she does not want to simply grant Bob access to the data nor respond with the real (clean) data, Bob requested. Thus, Bob and Alice agree on the following:
- Bob can ask any question, but
- Alice gives responses, which are to some degree randomised, yet probably close to the real data
While Bob gets useful approximate data as a response, he cannot deduce any individual information. The privacy of Alice’s customers is protected. The benefit of this approach is having both utility (for Bob) and privacy (for Alice and her customers). In the following it is going to be explained according to what principle Alice randomises her answers.
Randomization
In differential Privacy two variants of randomising information or adding noise exist:
- Adding noise to a response given to a request on the data
- Adding noise already in the process of collecting data
The following example shows how the second variant works. It deals with a simple survey in which people are asked to answer a polar question. As differential privacy preserves the respondents’ privacy the question could be sensitive, e.g. whether he/she takes drugs or has a specific disease.
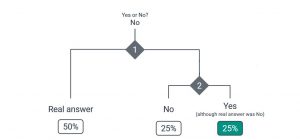
To determine what answer is stored for a respondent, a randomized experiment is performed twice. This experiment is independent from the respondent’s real answer and can be a coin toss in the simplest case. The outcome of the first experiment determines, whether the real answer is stored in the database of answers to this survey. With a 50 percent probability the real answer is stored. The other 50 percent of the time the randomized experiment is performed again.
The following second run of the experiment decides what answer is saved instead of the individual’s real answer: yes or no. With a 25 percent chance the stored answer can be Yes although he/she actually responded with No.
This method adds random errors to single measured values and has the effect of plausible deniability of every individual’s answer. This means that because of the added randomised noise respondents can deny having given the stored answer.
After collecting a large enough amount of respondents’ answers with added noise according to this variant, one would be able to gather approximate statistical values. As the proportion and distribution of noise is known, the amount of “wrong” answers can be compensated to get statistical values close to those based on data without noise. Yet only approximate, they are useful to the requesting party depending on their proximity to the “real” values (which in turn partly depend on the method of adding noise).
Using a coin toss to add noise is the simplest technique. More complex mathematical functions and distributions are used in sophisticated systems taking the approach of differential privacy (e.g. Laplace or Gaussian distribution).
Apple outlines the approach and effects of differential privacy in it’s “Technical Overview” as:
“[…] the idea that statistical noise that is slightly biased can mask a user’s individual data before it is shared with Apple. If many people are submitting the same data, the noise that has been added can average out over large numbers of data points, and Apple can see meaningful information emerge.”
By inserting noise, the differential privacy model guarantees that even if someone has complete information about 99 of 100 people in a data set, they still cannot deduce the information about the final person. For example, the 100th respondent’s answer to a polar question can still be yes or no, be it the real answer or simply the outcome of an experiment. An individual’s information is not determinable by an outsider only looking at the noisy data.
Furthermore, differential privacy relies on the fact that removing a single record from a large enough data collection has little impact on statistical values based on them. The impact shrinks with growing size of the collection. The probability of a result of the evaluation of the data would neither be increased nor decreased significantly if this particular person would refrain from providing its record. This addresses possible concerns of potential participant of the data collection. They might fear that an individual’s information could be disclosed or deduced. However, these concerns can be dispelled and motivation can be build more easily.
Definition of privacy in the context of differential privacy
This leads to a definition of privacy, here in the context of differential privacy:
Privacy of an individual is preserved if it makes no difference to a statistical request whether the data collection contains its specific record or not.
If this statement is met, one cannot deduce any individual’s information by comparing a statistical value based on the collection including the individual’s record to one not including it.
This is basically what the mathematical definition of differential privacy states.
Pr[ Κ(D1) ∈ E ] ≤ e? × Pr[ Κ(D2) ∈ E ]
D1 and D2 are so called neighboring data sets, differing in at most one element (informal definition: D2 := D1 – Person X). K is a function mapping the data sets to an output space S, E is a subset of S. K maps random records in D to noise. The inequation compares the probability of the mapping to one value (e.g. answer to a survey question) based on D1 (left side) to the probability of that mapping based on D2.
The only factor differing between the two sides is e?. The bigger the value of ? the bigger the right side of the inequation. This parameter ? describes to what extent the absence of one single record should affect statistical values or responses to requests at the maximum. To achieve a high level of privacy, ? must be kept as low as possible. It is a measure for the loss of privacy.
Privacy budget
? is also called the privacy budget, as queries or requests on the data collection can be limited by granting certain values for ?. Each query has an assigned value for ?, based on the question: How much could an attacker learn about anyone from this query? Thus, it is measuring privacy loss.
A query which has a higher amount of obtainable knowledge about individuals requires a lower value for ?. Privacy budget must be granted carefully, since
- it adds up with queries: Two queries with ? = 1 add up to ? = 2
- it grows exponentially: A query assigned with ? = 1 is almost 3 times more private than one with ? = 2 and more than 8,000 times more private than with ? = 10.
Though, the consequence of a higher preservation of privacy is a lower level of accuracy (or worse approximation) of statistical values.
| High ? | Low ? | |
| Accuracy | High | Low |
| Privacy | Low | High |
An advantage of the approach of differential privacy is that it reduces the tradeoff between accuracy/utility on the one hand and privacy on the other hand to one key ratio represented by ?. Some experts in theoretical computer science and data protection recommend values between zero and one for ? for a good level of privacy and say one to ten is still acceptable. They advise against values higher than ten, as privacy is significantly decreased granting requests with a budget higher than this.
Variants
As stated earlier, noise can be added at two different points in the overall process of data collection and analyzation.
The method described above, namely adding noise already when collecting the data (randomizing some of the answers to a polar question in a survey) is part of a variant of differential privacy called “locally private”. An advantage of this is that the participant already adds the noise himself. Thus, the analyzing party can only see noisy data, and does not need to be trusted. However, because the information is noisy statistical values are usually less accurate than when using clean data. As noise is added in the very first step of collection and after that only noisy data exists, the safety of the information is high.
In contrast to this approach stands one called “globally private”. A curator collects (clean) data and adds noise to the whole, usually when giving a response. The participants need to trust in him performing the process correctly. Since the curator can operate on clean data, the accuracy is higher than in the locally private method. The safety however is lower, because trust is needed, and the curator is a single point of failure.
Application
Large companies like Apple and Google have adopted techniques of differential privacy into their systems and software. Apple uses the approach since iOs 10 and macOS Sierra for various purposes:
It is used in the Safari browser to monitor displaying which websites consumes a large amount of battery power. Yet, using the approach of differential privacy Apple cannot track visited websites per individual user. Furthermore, Apple tries to analyze, which words are typed in which context to improve their word recommendation service on the iOs keyboard, the same goes for emoji usage.
Google implemented the approach of differential privacy in an open source library and published it on github for everyone to integrate in their own system. It is called Randomized Aggregable Privacy Preserving Ordinal Response, in short RAPPOR. They use this library in the Chrome browser to monitor which and how other software changes browser settings since 2014. The goal is to detect malware. Google also uses techniques from differential privacy in Google Maps to observe traffic density and integrate this information into planned routes.
Conclusion
Differential privacy is a promising approach giving a mathematical guarantee for privacy. However it is not suitable and usable for all kinds of data. It works best with a large amount of records containing numeric data or a little limited number of possible answers (for example: yes/no or 1 to 5). Other types of data like images or audio recordings would be made useless adding noise to it.
It is already well researched theoretically, but not yet strongly/widely used in practice. A reason for that could be higher implementation costs compared to classic anonymization techniques.
Discussion
Series of data points
Regarding existing applications of differential privacy, location pattern mining (such as in Google Maps) draws attention. Differential privacy seems useful in this context at first, as it addresses the users’ possible concern of exposing the current location to Google and related companies. At first sight it seems impossible for anyone else but you to access your current location (using the locally private variant) or anyone but the collecting party (here: Google, in the globally private approach).
However, information about location is probably obtained as a series of data points. Therefore, it is practically possible to detect a progression and outliers added into the series by a randomization function. Thus, users’ individual exact location history can be made accessible.
Correlation
The theoretic approach of differential privacy works for single questions or requests. However, often questions do not stand alone, like in a questionnaire or another form of a survey. From an amount of questions related to one topic, correlation and repeating patterns can be drawn. This allows building models for example according to social stereotypes. Again, outliers from patterns and typical models can be detected as they are less likely to be given in the context of answers. Thus, privacy would be violated.
Besides, combining multiple requests on data sources querying different but connectable or correlatable information can be used to deduce information about individuals one would not have been able to see as “clean data” otherwise.
Collusion
A similar issue to the one with correlatable data exists with collusion. Users can agree on making similar requests and combining them afterwards. Thereby they can achieve a higher privacy budget than they were originally granted.
Privacy Budget
This leads to the question of defining the right privacy budget. It needs to be researched whether a static definition per user suffices or a dynamic definition would be more reasonable and more secure. This in turn gives rise to the next question, namely which parameters should be considered when defining a dynamic privacy budget.
All in all, differential privacy looks like a good approach on tackling privacy issues in some, but not all cases. It depends on the type of data collected, the amount of information stored and correlation between it. Defining and granting privacy budget should be carefully thought out, as it can be misused in the ways described above.
For anyone interested in the mathematical basis and proofs underlying the approach of differential privacy, I suggest reading “The Algorithmic Foundations Of Differential Privacy” (Cynthia Dwork, Microsoft Research, USA and Aaron Roth, University of Pennsylvania, USA).
Sources
Dwork C. (2006) Differential Privacy. In: Bugliesi M., Preneel B., Sassone V., Wegener I. (eds) Automata, Languages and Programming. ICALP 2006. Lecture Notes in Computer Science, vol 4052. Springer, Berlin, Heidelberg; https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/dwork.pdf (28.06.18)
Differential Privacy – Simply Explained by User “Simply Explained – Savjee” on Youtube; https://www.youtube.com/watch?v=gI0wk1CXlsQ (28.06.18)
Differential Privacy Technical Overview, Apple; https://images.apple.com/privacy/docs/Differential_Privacy_Overview.pdf (28.06.18)
Tore Dalenius.Towards a methodology for statistical disclosure control. Statistik Tidskrift, 15(429-444):2, 1977.
Benett Cyphers. Understanding differential privacy and why it matters for digital rights (25.10.2017); https://www.accessnow.org/understanding-differential-privacy-matters-digital-rights/ (28.06.18)
Tianqing Zhu. Explainer: what is differential privacy and how can it protect your data? (18.03.2018); https://theconversation.com/explainer-what-is-differential-privacy-and-how-can-it-protect-your-data-90686 (28.06.18)

Leave a Reply
You must be logged in to post a comment.