Ergodicity Explained

Ergodicity is an attribute a system can either possess or lack. According to Peters, ergodicity requires the following conditions:

We will call an observable ergodic if its time average equals its expectation value, that is if it satisfies Birkhoff’s equation

[1] Ole Peters: The ergodicity problem in economics

To illustrate this point without just dissecting a math equation, let’s examine a thought experiment.

Imagine you’re playing a gambling game in which you pay 3€ to roll a 6-sided die and deduct one from the result, and at the end, you get the payout of the rolled result in euros. However, you can only play the game once and you have to determine how often you want to roll in advance and pay the fee for each roll in advance. Let’s say you decide to roll six times in a row. 3.5 is the average result of a 6-sided die, which means you are expected to lose 0.5€⁽¹⁾ euros per roll as you subtract 1 from the result of the die. With 6 runs of this game, the expected loss is 3€⁽²⁾.

<em>(1): 3.5 - 1 - 3 = -0.5€
(2): 6 * (-0.5) = -3€</em>

Cool, we can do some basic math, but what does ergodicity have to do with any of this? That’s the interesting part, if we look at this game as a system it would fulfill the condition necessary to be ergodic. The outcome is the same whether you play the game 6 times in a row or get 5 friends together and each plays 1 round simultaneously. (Assuming of course your friends play using your money and give you back all profits.)

In other words, a system is ergodic when the average outcome over a time series (time probability) is the same as the outcome of parallel events (ensemble probability).

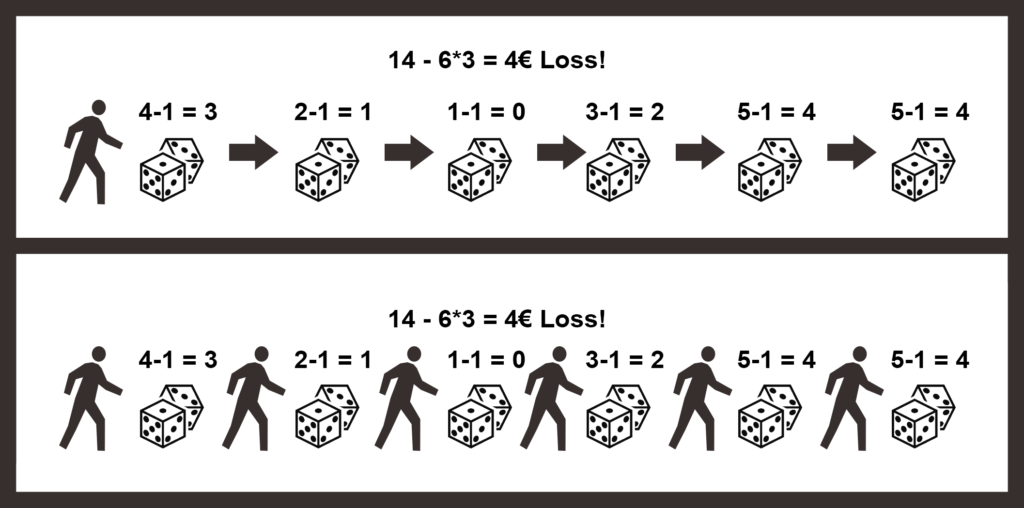
The nice thing about ergodic systems is that it is relatively easy to calculate what outcomes a person can expect from the system over time: just average the probability-based results and extrapolate them over time. 

As you can imagine, most systems do not meet this criterion and therefore are not ergodic. As an example, if we rework the dice-throwing experiment and instead multiplied the payout value from the previous throw instead of adding it, starting from 1€ as the initial payout value, the average outcome of 1 person playing six times in a row will be drastically different from 6 people playing just once. 

If we examine the outcomes of my parallel players, the adapted experiment still has predictable results. If, however, we look at an individual who plays a series of games we see that every round we can expect an increase of 250%⁽³⁾ in rewards. This means that after six rounds the payout should be 226€⁽⁴⁾

(3): (1/6) * 1 * (1 - 1) + (1/6) * 1 * (2 - 1) + (1/6) * 1 * (3 - 1) + (1/6) * 1 * (4 - 1) + (1/6) * 1 * (5 - 1) + (1/6) * 1 * (6 - 1) = 2.5
(4): 1 * 2.5<sup>6</sup> = 244 - 18 = 226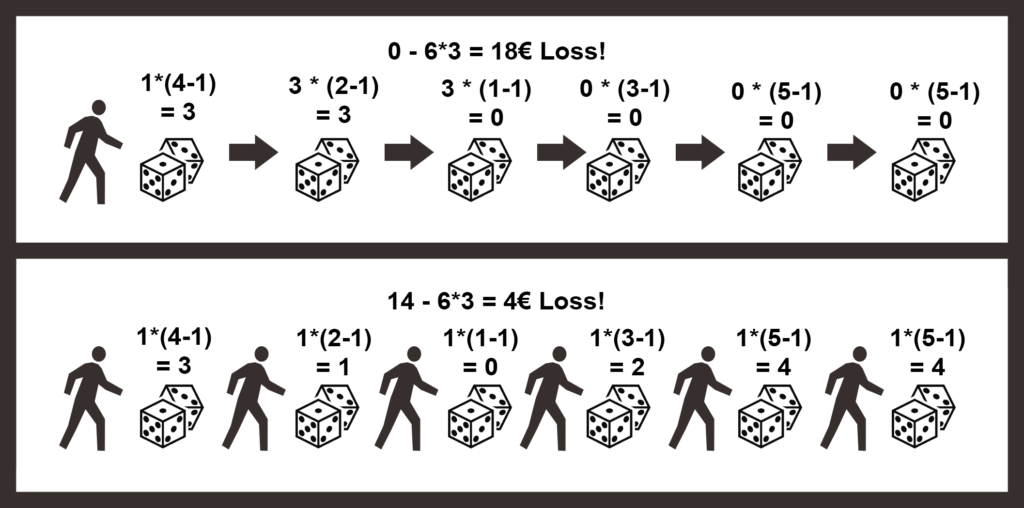

From an intuitive standpoint this may not make any sense; the more you play, the higher your chances are of rolling a 1 and ultimately entering what Taleb calls the state of “Ruin” from which you can no longer recover. So, then, why would our formula predict high gains on average? In a non-ergodic game, results are more likely to tend towards extremes, either hitting 0 and never recovering or multiplying exponentially for a huge payout of potentially 15607€⁽⁵⁾

(5): 1 * 5<sup>6</sup> = 15625 - 18 = 15607

The Problem of ignoring Ergodicity

Although the average result of the above experiment sounds very promising, the majority of participants are going to lose money. Only about 33%⁽⁶⁾ of players are statistically likely to not roll a 1 during 6 rolls. The longer a player plays the game, the worse the phenomenon becomes. The odds of not rolling a 1 at 100 rolls are as low as 0.0000012%⁽⁷⁾, but the rewards also increase exponentially. The longer the game, the higher the expected payout according to our formula, while in reality the “average” or most common expectable result for the vast majority of the players is going to be a loss of money.

(6): (5/6)<sup>6</sup> = 0.33
(7): (5/6)<sup>100</sup> = 0.000000012

This example might make it more obvious why treating non-ergodic systems the same way as ergodic ones is a problem, specifically in economics. Would you ever play the prior game if they had to play 100 rounds? I certainly would not, since, despite the potential exorbitant outcome, I am almost guaranteed to lose money. Yet our formula makes the prediction that on average we are sure to win money. In an article about ergodicity, Taleb even states that non-ergodic systems, due to the existence of ruin states cant be properly evaluated.

I effectively organized all my life around the point that sequence matters and the presence of ruin does not allow cost-benefit analyses; but it never hit me that the flaw in decision theory was so deep. Until came out of nowhere a paper by the physicist Ole Peters … and showed that about everything in social science about probability is flawed. Deeply flawed. Very deeply flawed.

[2] Nassim Nicholas Taleb: The Logic of Risk Taking

Taleb refers to “The ergodicity problem in economics,” a paper written by Ole Peters and published in a nature journal. This paper is at the root of the critics’ attacks on the current economic paradigm. 

This paper argues that a fundamental component of economic theory, “expected utility theory”, is flawed because it makes an indiscriminate assumption of ergodicity. In other words, the theory can be applied only to ergodic systems, and the systems that it is applied to are assumed to be ergodic systems. 

At a crucial place in the foundations of economics, it is assumed that the answer is always yes — a pernicious error.

[1] Ole Peters: The ergodicity problem in economics

Peters goes on to explain that financial advice based on these principles leads to nonsensical predictions because wealth is non-ergodic, and errors from these predictions are fixed with psychological arguments blaming humans for irrational behavior.

Scientifically, this deserves some reflection: the models were exonerated by declaring the object of study irrational.

[1] Ole Peters: The ergodicity problem in economics

Finally, Peters offers a solution to the problem plaguing economics. Replacing the deprecated “Expected Utility Theory” with a Growth Rate optimization algorithm called Ergodicity Economics, which does a better job of predicting how our wealth will develop over time. We can calculate expected results using Ergodicity Economics by calculating a log growth rate. In our experiment, the expected growth rate of our game would be -∞⁽⁸⁾.

(8): 1/6 * log(1-1) + 1/6 * log(2-1) + 1/6 * log(3-1) + 1/6 * log(4-1) + 1/6 * log(5-1) + 1/6 * log(6-1) = -∞

The expected result of playing the game over a time series is that we lose our cash.

Conclusion

As distrust for our current established institutions grows, Peters’s and Taleb’s scathing critiques of the current economic status quo have become increasingly popular. There is no doubt that thousands of people now feel vindicated in their opinion that capitalism has failed them, with one of the main institutions entrusted with its promotion and understanding being so horribly flawed at a fundamental level.

Though one thing does not quite make sense to me…

Pages: 1 2 3